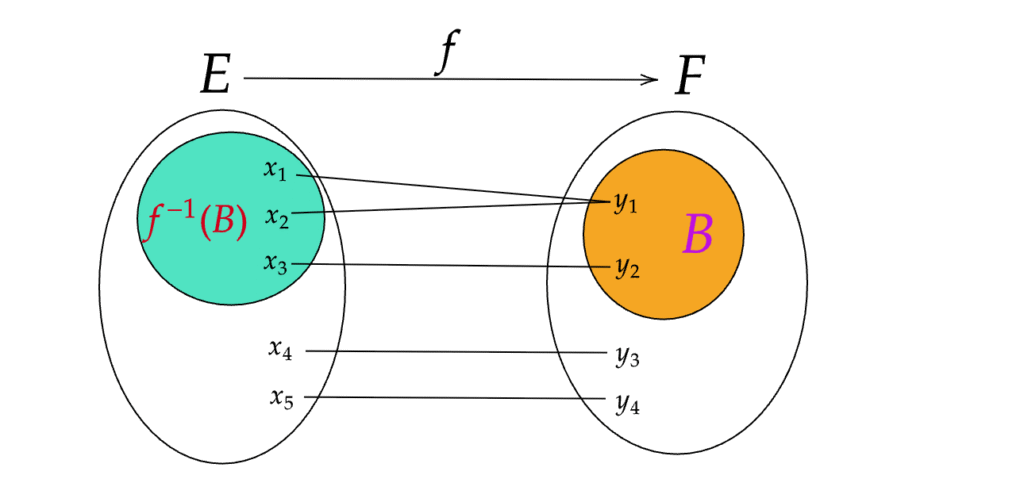
On appelle image réciproque d’un ensemble \( B \subset F \) par une application \( f \ : \ E \rightarrow F \) l’ensemble des antécédents des éléments B par l’application \( f \), on la note \( f^{-1}(B) \).
En notation mathématique : \( f^{-1}(B)= \left\{ x \in E \mid f(x) \in B \right\} \)
Exemples illustrant l’image réciproque :
Exemple 1 :
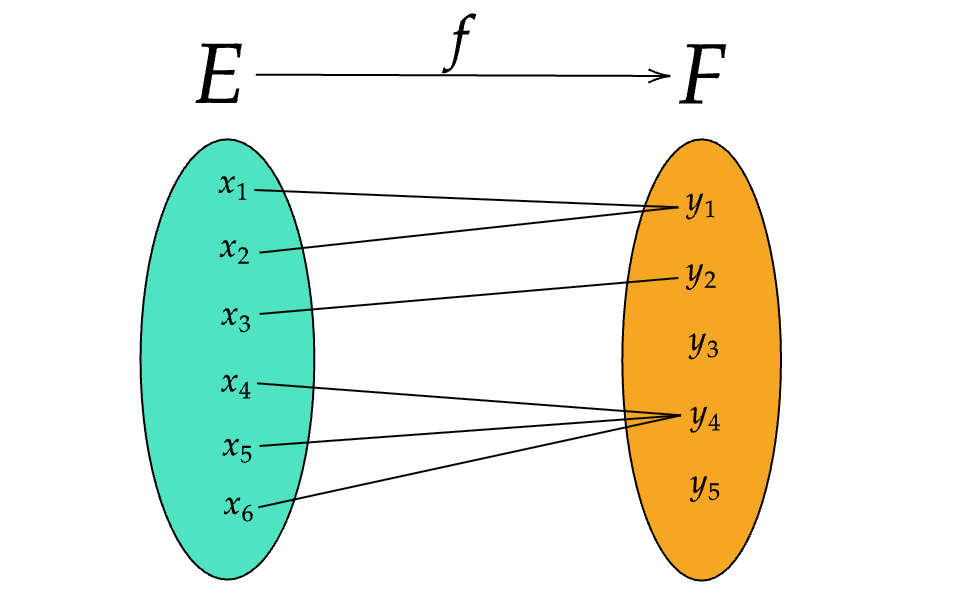
Dans cet exemple \( f \) est une application d’un ensemble \( E= \left\{ x_{1};x_{2};x_{3};x_{4};x_{5};x_{6} \right\} \) dans un ensemble \( F= \left\{ y_{1};y_{2};y_{3};y_{4};y_{5} \right\} \) telle que \( f(x_{1})=f(x_{2})=y_{1} \) et \( f(x_{3})=y_{2} \) et \( f(x_{4})=f(x_{5})=f(x_{6})=y_{4} \)
Voici ce que l’on obtient :
- \( f^{-1}(\left\{y_{1}\right\})= \left\{ x_{1};x_{2} \right\} \)
- \( f^{-1}(\left\{y_{2}\right\})= \left\{ x_{3} \right\} \)
- \( f^{-1}(\left\{y_{3}\right\})= \emptyset = f^{-1}(\left\{y_{5}\right\}) \)
- \( f^{-1}(\left\{y_{4}\right\})= \left\{ x_{4};x_{5};x_{6} \right\} \)
- \( f^{-1}(\left\{ y_{1} ;y_{2};y_{3}\right\})= \left\{ x_{1};x_{2};x_{3} \right\} \)
- \( f^{-1}(\left\{ y_{1} ;y_{2};y_{4}\right\})= E \)
Exemple 2 :
On considère l’application \( f \ : \
\begin{array}{lll}
\mathbb{N} \to \mathbb{N} \\
n \mapsto 2n+1
\end{array}
\)
On obtient dans cet exemple :
- \( f^{-1}( \left\{ 1 \right\} )= \left\{ 0 \right\} \)
- \( f^{-1}( Ensemble \ des \ nombres \ impairs )= \mathbb{N} \)
- \( f^{-1}( Ensemble \ des \ nombres \ pairs )= \emptyset \)
Propriétés de l’image réciproque :
Propriété 1 :
Soient \( E \) et \( F \) deux ensembles, \( B \) une partie de \( F \) et \( f \) une application de \( E \) dans \( F \).
On a les propriétés suivantes :
- \( f^{-1}(B) \subset E \)
- \( \forall x \in E, \ x \in f^{-1}(B) \Leftrightarrow f(x) \in B \)
- \( f^{-1}(\emptyset)= \emptyset \)
- \( f^{-1}(F)=E \)
Propriété 2 :
Soient E et F deux ensembles non vides, et \( f \) une application de E dans F.
On a les propriétés suivantes :
- \( \forall A,B \in \mathcal{P}(F), \ A \subset B \Rightarrow f^{-1}(A) \subset f^{-1}(B) \)
- \( \forall A,B \in \mathcal{P}(F), \ f^{-1}(A \cup B ) =f^{-1}(A) \cup f^{-1}(B) \)
- \( \forall A,B \in \mathcal{P}(F), \ f^{-1}(A \cap B ) =f^{-1}(A) \cap f^{-1}(B) \)
- \( \forall A \in \mathcal{P}(F), \ f^{-1} ( C^{A}_{F})= C^{f^{-1}(A)}_{E} \)
Exercices sur l’image réciproque d’un ensemble :
Exercice 1
On considère l’application \( f \ : \
\begin{array}{lll}
\mathbb{R^{2}} \to \mathbb{R} \\
(x,y) \mapsto (x-1)^2 +y^2
\end{array}
\)
Calculer \( f^{-1}(\{0\}) \), \( f^{-1}(\;]-\infty , 1[\;) \) et \( f^{-1}(\{4\}) \)
Indications
Corrigé
Exercice 2
On considère l’application \( f \ : \
\begin{array}{lll}
\mathbb{R^{+}} \to \mathbb{R} \\
x \mapsto x-2 \sqrt x
\end{array}
\)
Déterminer \( f^{-1}(\;[-1 , 0]\;) \) l’image réciproque de l’intervalle [-1, 0] par la fonction \( f \).
