Dans cet article, nous présentons la formule de la dérivée de Arccos, puis nous en donnons une démonstration détaillée.
Enfin, nous illustrons cette formule à travers plusieurs exemples de dérivation de fonctions composées de la forme \(Arccos(u(x))\), où \(u\) est une fonction donnée.
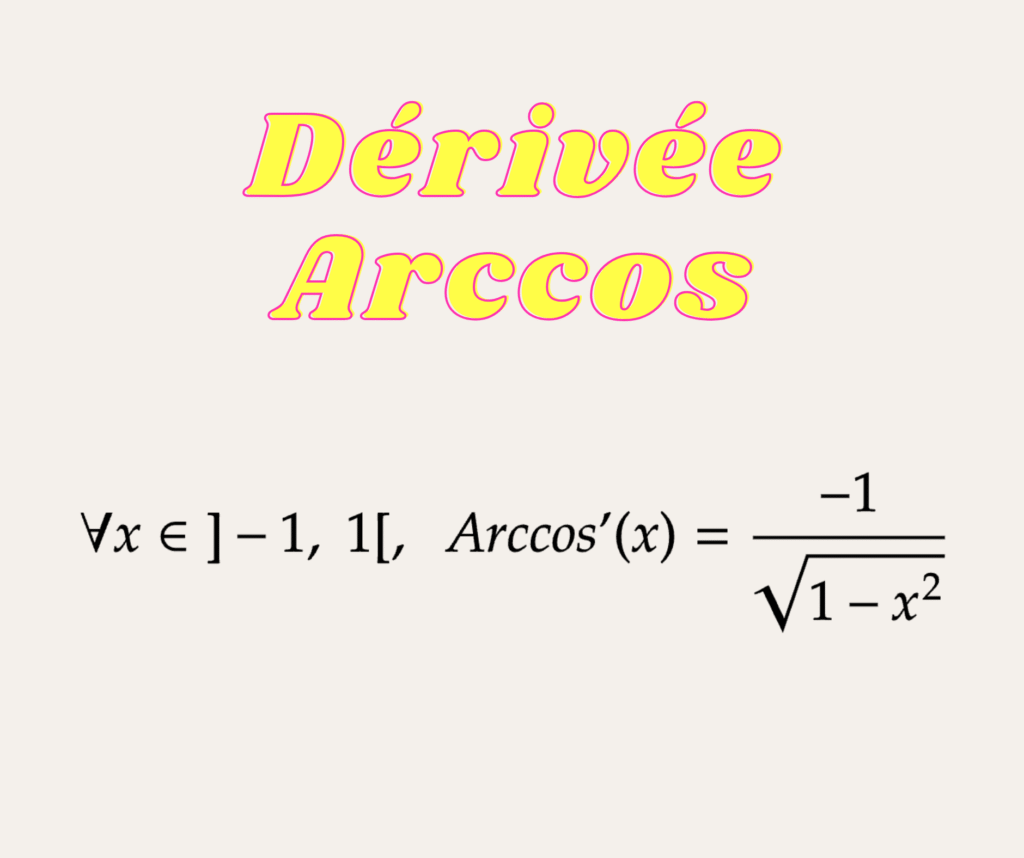
1) Formule de la dérivée de Arccos
La fonction arccosinus est dérivable sur l’intervalle \( ]-1,1[ \), et sa dérivée est donnée par la formule :
\[
\forall x \in ]-1,1[, \quad \text{Arccos}'(x) = \frac{-1}{\sqrt{1 – x^2}}
\]
2) Démonstration de la formule de la dérivée de Arccos
Commençons par justifier que Arccos est dérivable sur \( ]-1,1[ \).
Tout d’abord, la fonction Arccos est la bijection réciproque de la restriction de la fonction cosinus à l’intervalle \( [0, \pi] \). Autrement dit, \( \text{Arccos} = (\cos_{|[0, \pi]})^{-1} \).
Par conséquent, la fonction arccosinus est définie sur \( [-1,1] \) et prend ses valeurs dans \( [0, \pi] \), c’est-à-dire : \( \text{Arccos} : [-1,1] \rightarrow [0, \pi] \).
Or, on sait que la fonction cosinus est dérivable sur \( [0, \pi] \), et que \( \forall x \in [0, \pi], \quad \cos'(x) = -\sin(x)
\)
De plus, la dérivée de cosinus, soit \(-\sin(x)\), ne s’annule pas sur \( ]0, \pi[ \), et on a \( \cos(]0, \pi[) = ]-1,1[ \).
Par le théorème des fonctions réciproques, la fonction Arccos est donc dérivable sur \( ]-1,1[ \).
Cherchons maintenant la formule de la dérivée de Arccos. On a :
\(
\forall x \in ]-1,1[, \quad \text{Arccos}'(x) = \left( \left( \cos_{|[0,\pi]} \right)^{-1} \right)'(x)
\)
Toujours par le théorème des fonctions réciproques :
\(
\begin{aligned}
\forall x \in ]-1,1[, \quad \text{Arccos}'(x) &= \frac{1}{\cos'(\text{Arccos}(x))} \\
&= \frac{1}{- \sin(\text{Arccos}(x))}
\end{aligned}
\)
Puisque \( \forall x \in ]-1,1[ \), on a \( \text{Arccos}(x) \in ]0, \pi[ \), donc :
\(
\sin(\text{Arccos}(x)) = \sqrt{1 – \cos^2(\text{Arccos}(x))} = \sqrt{1 – x^2}
\)
D’où : \( \forall x \in ]-1,1[, \quad \text{Arccos}'(x) = \frac{-1}{\sqrt{1 – x^2}}
\)
Ce qui achève la preuve de la formule.
Remarque : La dérivée de Arccos est strictement négative, donc Arccos est strictement décroissante sur \( ]-1,1[ \).
3) Dérivée de Arccos u où u est une fonction dérivable
Soit \( u \) une fonction dérivable sur un intervalle \( I \subset \mathbb{R} \) telle que \( u(I) \subset ]-1,1[ \).
Par la formule de la dérivée d’une composée, la fonction \( x \mapsto \text{Arccos}(u(x)) \) est dérivable sur \( I \) et :
\[
\forall x \in I, \quad \left( \text{Arccos}(u(x)) \right)’ = \frac{ -u'(x) }{ \sqrt{1 – u(x)^2} }
\]
Voici quelques exemples :
- \( \forall x \in ]-1,1[, \quad \left( \text{Arccos}(x^2) \right)’ = \frac{ -2x }{ \sqrt{1 – x^4} } \)
- \( \forall x \in ]-\frac{1}{2}, \frac{1}{2}[, \quad \left( \text{Arccos}(2x) \right)’ = \frac{ -2 }{ \sqrt{1 – 4x^2} } \)
