En mathématiques, un produit télescopique est un produit de la forme \( \displaystyle \prod_{k=p}^{n} \frac{a_{k+1}}{a_{k}} \) où \( \left(a_{k}\right)_{k \in \mathbb{N}} \) est une suite de nombres réels ou complexes qui ne s’annule pas.
Il s’agit donc d’un produit dont chaque terme est le quotient de deux termes consécutifs d’une même suite.
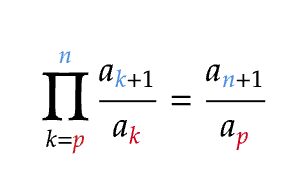
Formule du produit télescopique :
Si \( \left(a_{k}\right)_{k \in \mathbb{N}} \) est une suite qui ne s’annule pas, de nombres réels ou complexes, alors on a la formule suivante : \( \displaystyle
\prod_{k=p}^{n} \frac{a_{k+1}}{a_{k}} = \frac{a_{n+1}}{a_{p}}
\)
Démonstration :
\( \displaystyle
\begin{aligned}
\prod_{k=p}^{n} \frac{a_{k+1}}{a_{k}}
&= \frac{\prod_{k=p}^{n} a_{k+1}}{\prod_{k=p}^{n} a_{k}} \\
&= \frac{\prod_{k=p+1}^{n+1} a_{k}}{\prod_{k=p}^{n} a_{k}} \\
&= \frac{a_{n+1} \prod_{k=p+1}^{n} a_{k}}{a_{p} \prod_{k=p+1}^{n} a_{k}} \\
&= \frac{a_{n+1}}{a_{p}}
\end{aligned}
\)
Dans la formule \( \displaystyle \prod_{k=p}^{n} \frac{a_{k+1}}{a_{k}} = \frac{a_{n+1}}{a_{p}} \), le télescopage vient du fait que les termes «intérieurs» se simplifient.
Voici un exemple simple :
\( \displaystyle
\begin{aligned}
\prod_{k=1}^{5} \frac{a_{k+1}}{a_{k}}
&= \frac{a_{2}}{a_{1}} \cdot \frac{a_{3}}{a_{2}} \cdot \frac{a_{4}}{a_{3}} \cdot \frac{a_{5}}{a_{4}} \cdot \frac{a_{6}}{a_{5}} \\
&= \frac{a_{6}}{a_{1}}
\end{aligned}
\)
Tous les termes se simplifient entre eux sauf \( a_{1} \) et \( a_{6} \).
Produit télescopique : Exemples
Voici quelques exemples de produits télescopiques :
- \( \displaystyle \prod_{k=p}^{n} \frac{a_{k-1}}{a_{k}} = \frac{a_{p-1}}{a_{n}} \)
- \( \displaystyle \prod_{k=p}^{n} \frac{a_{k+2}}{a_{k+1}} = \frac{a_{n+2}}{a_{p+1}} \)
- \( \displaystyle \prod_{k=p}^{n} \frac{k+1}{k} = \frac{n+1}{p} \)
- \( \displaystyle \prod_{k=2}^{n} \frac{\ln(k+1)}{\ln(k)} = \frac{\ln(n+1)}{\ln(2)} \)
Exercices corrigés sur les produits télescopiques
Exercice 1 ⭐️
Soit \( n \) un entier supérieur à 1. Calculer \( \displaystyle \prod_{k=1}^{n} \left(1 + \frac{1}{k}\right) \)
Indications
Utiliser un télescopage
Corrigé
\( \displaystyle
\begin{aligned}
\prod_{k=1}^{n} \left(1 + \frac{1}{k} \right)
&= \prod_{k=1}^{n} \frac{k+1}{k} \\
&= \frac{n+1}{1} \\
&= n+1
\end{aligned}
\)
Exercice 2 ⭐️
Soit \( n \) un entier supérieur à 2. Calculer \( \displaystyle \prod_{k=2}^{n} \left(1 – \frac{1}{k^{2}} \right) \)
Indications
Utiliser un produit télescopique pour simplifier l’expression.
Corrigé
\( \displaystyle
\begin{aligned}
\prod_{k=2}^{n} \left(1 – \frac{1}{k^2} \right)
&= \prod_{k=2}^{n} \frac{k^2 – 1}{k^2} \\
&= \prod_{k=2}^{n} \frac{(k-1)(k+1)}{k \cdot k} \\
&= \left( \prod_{k=2}^{n} \frac{k-1}{k} \right) \left( \prod_{k=2}^{n} \frac{k+1}{k} \right) \\ &= \frac{1}{n} \cdot \frac{n+1}{2} \quad \text{(par télescopage)} \\
&= \frac{n+1}{2n}
\end{aligned}
\)
Exercice 3 ⭐️
Soient \( a \in\, ]0, \pi[ \) et \( n \in \mathbb{N}^* \). Calculer \( \displaystyle \prod_{k=1}^{n} \cos \left( \frac{a}{2^k} \right) \)
Indications
Utiliser la formule \( \sin(2x) = 2 \cos(x) \sin(x) \).
Corrigé
On utilise la formule \( \sin(2x) = 2 \cos(x) \sin(x) \).
\( \displaystyle
\begin{aligned}
\prod_{k=1}^{n} \cos\left( \frac{a}{2^k} \right)
&= \prod_{k=1}^{n} \frac{\sin\left(2 \cdot \frac{a}{2^k} \right)}{2 \sin\left( \frac{a}{2^k} \right)} \\
&=\frac{1}{2^{n}} \prod_{k=1}^{n} \frac{\sin\left( \frac{a}{2^{k-1}} \right)}{ \sin\left( \frac{a}{2^k} \right)} \\
&= \frac{1}{2^n} \cdot \frac{\sin(a)}{\sin\left( \frac{a}{2^n} \right)} \quad \text{(par télescopage)} \\
&= \frac{\sin(a)}{2^n \sin\left( \frac{a}{2^n} \right)}
\end{aligned}
\)
Exercice 4 ⭐️
Soit \( n \in \mathbb{N} \). Calculer \( \displaystyle \prod_{k=0}^{n} \frac{k^2 + 5k + 6}{k^2 + 5k + 4} \)
Indications
Utiliser un produit télescopique
Corrigé
\( \displaystyle
\begin{aligned}
\prod_{k=0}^{n} \frac{k^2 + 5k + 6}{k^2 + 5k + 4}
&= \prod_{k=0}^{n} \frac{(k+2)(k+3)}{(k+1)(k+4)} \\
&= \left( \prod_{k=0}^{n} \frac{k+2}{k+1} \right) \left( \prod_{k=0}^{n} \frac{k+3}{k+4} \right) \\
&= \frac{n+2}{1} \cdot \frac{3}{n+4} \\
&= \frac{3(n+2)}{n+4}
\end{aligned}
\)
Exercice 5 ⭐️
Soit \( n \) un entier supérieur ou égal à 3. Calculer \( \displaystyle \prod_{k=3}^{n} \frac{k^2 – k – 2}{k^2 + 2k – 3} \)
Indications
Appliquer des produits télescopiques pour simplifier l’expression
Corrigé
\( \displaystyle
\begin{aligned}
\prod_{k=3}^{n} \frac{k^2 – k – 2}{k^2 + 2k – 3}
&= \prod_{k=3}^{n} \frac{(k-2)(k+1)}{(k-1)(k+3)} \\
&= \left( \prod_{k=3}^{n} \frac{k-2}{k-1} \right) \left( \prod_{k=3}^{n} \frac{k+1}{k+3} \right) \\
& =\frac{3-2}{n-1} \prod_{k=3}^{n} \frac{(k+1)(k+2)}{(k+2)(k+3)} \quad \text { (par télescopage) } \\
&= \frac{1}{n-1} \cdot \frac{4 \cdot 5}{(n+2)(n+3)} \text { (par télescopage) } \\
&= \frac{20}{(n-1)(n+2)(n+3)}
\end{aligned}
\)
